Many solutions contain one component, called the solvent, in which other components, called solutes, are dissolved. An aqueous solution is one for which the solvent is water. The concentration of a solution is a measure of the relative amount of solute in a given amount of solution.
Concentrations may be measured using various units, with one very useful unit being molarity, defined as the number of moles of solute per liter of solution. The solute concentration of a solution may be decreased by adding solvent, a process referred to as dilution. The dilution equation is a simple relation between concentrations and volumes of a solution before and after dilution. An aqueous solution consists of at least two components, the solvent and the solute . Usually one wants to keep track of the amount of the solute dissolved in the solution. One could do by keeping track of the concentration by determining the mass of each component, but it is usually easier to measure liquids by volume instead of mass.
Molarity is defined as the number of moles of solute divided by the volume of the solution in liters. For example, the known molecular weight of a chemical can be used along with the desired solution volume and solute concentration to determine the mass of chemical needed to make such a solution. As with w/v solutions, we weigh out a specific amount of chemical when making a molar solution. Unlike w/v solutions, the amount to weigh depends on the molecular weight (m.w.) of the substance in grams per mole (g/mol). In order to calculate the desired mass of solute you will need to know the formula weight.
Formula weights are usually printed on the label and identified by the abbreviation f.w. Formula weight is the mass of material in grams that contains one mole of substance, and may include inert materials and/or the mass of water molecules in the case of hydrated compounds. For pure compounds the formula weight is the molecular weight of the substance and may be identified as such. The concentration of a substance is the quantity of solute present in a given quantity of solution. Concentrations are usually expressed as molarity, the number of moles of solute in 1 L of solution. Figure 4.6 "Preparation of a Solution of Known Concentration Using a Solid Solute" illustrates this procedure for a solution of cobalt chloride dihydrate in ethanol.
Because the solute occupies space in the solution, the volume of the solvent needed is almost always less than the desired volume of solution. For example, if the desired volume were 1.00 L, it would be incorrect to add 1.00 L of water to 342 g of sucrose because that would produce more than 1.00 L of solution. As shown in Figure 4.7 "Preparation of 250 mL of a Solution of (NH", for some substances this effect can be significant, especially for concentrated solutions. It is important to note that the molarity is defined as moles of solute per liter of solution, not moles of solute per liter of solvent.
This is because when you add a substance, perhaps a salt, to some volume of water, the volume of the resulting solution will be different than the original volume in some unpredictable way. To get around this problem chemists commonly make up their solutions in volumetric flasks. These are flasks that have a long neck with an etched line indicating the volume.
The solute is added to the flask first and then water is added until the solution reaches the mark. The flasks have very good calibration so volumes are commonly known to at least four significant figures. To calculate the molarity of a solution, the number of moles of solute must be divided by the total liters of solution produced. Suppose that someone has already worked out the details, so all that you have to do is read a formula and make a solution. We can usually assume that a solution is to be aqueous unless stated otherwise. What about the concentration of the substance to be added?
Common ways of describing the concentrations of solutions are weight-in-weight, weight-in-volume, volume-in-volume, and molarity. Less commonly used descriptions include normality and molality. A quantity of solute is measured out, mixed with solvent, and the volume is brought to some final quantity after the solute is completely dissolved. That is, solutions are typically prepared volumetrically.
Because solutes add volume to a quantity of solvent, this method of preparation of solutions is necessary to ensure that an exact desired concentration is obtained. To calculate the molarity of a solution, the number of moles of solute must be divided by the total liters of the solution produced. V is volume of solution in liters in which the indicated mass of solute must be dissolved to make the desired molar concentration . Note that V is the final or total volume of solution after the solute has been added to the solvent. A disadvantage of describing formulas as w/v (%) is that the description says nothing about the actual concentration of molecules in solution.
What if we want equal amounts of two chemicals to be mixed together, so that for each molecule of substance #1 there is a single molecule of substance #2? The same amount in grams will likely not contain the same number of molecules of each substance. For example, you may work with a chemical that can be in one of several forms of hydration. Calcium chloride can be purchased as a dry chemical in anhydrous form, so that what you weigh out is nearly all pure calcium chloride.
On the other hand you may have a stock of dry chemical that is hydrated with seven water molecules per molecule of calcium chloride. The same mass of this chemical will contain fewer molecules of calcium chloride. When we are interested in the actual concentration of molecules of a chemical in solution, it is better to have a universal measurement that works regardless of how the chemical is supplied. As long as the molecular weight is known, we can describe a solution in the form of moles per liter, or simply molar . While molality can be quite useful as a measurement of concentration, it isn't too convenient for converting to molarity.
The reason is that we usually don't know how much volume the solute is going to occupy in the solution. For example, when 900 ml of distilled H2O is mixed with 100 ml of ethanol , the total volume of the resulting aqueous solution will be less than 1 liter. The ethanol molecules are capable of organizing H-bonded water molecules tightly around them, resulting in a smaller volume than the combined volumes of the separate components.
In the solid, crystalline form glucose molecules are also ordered into a three dimensional array, as in the case of the NaCl crystal lattice discussed above. However, unlike in the case of NaCl, in which the compound breaks apart into smaller components , the glucose molecule remains intact as a single molecular unit in solution. The figure below is a schematic of the glucose molecule dissolved in water. Each glucose molecule is surrounded by a certain number of water molecules; therefore in solution, the glucose solid broke apart, but the glucose molecules themselves remained intact. Note that the definitions of molarity, molality, and mole fraction are the same for both molecular and nonmolecular solutions. You will learn more about interactions between molecules in Chemistry 111.
A schematic of the glucose molecule in aqueous solution. Concentrations are often reported on a mass-to-mass (m/m) basis or on a mass-to-volume (m/v) basis, particularly in clinical laboratories and engineering applications. Each measurement can be expressed as a percentage by multiplying the ratio by 100; the result is reported as percent m/m or percent m/v. For aqueous solutions at 20°C, 1 ppm corresponds to 1 μg per milliliter, and 1 ppb corresponds to 1 ng per milliliter. These concentrations and their units are summarized in Table 4.1 "Common Units of Concentration".
Molality is an intensive property of solutions, and it is calculated as the moles of a solute divided by the kilograms of the solvent. Unlike molarity, which depends on the volume of the solution, molality depends only on the mass of the solvent. Since volume is subject to variation due to temperature and pressure, molarity also varies by temperature and pressure. In some cases, using weight is an advantage because mass does not vary with ambient conditions. For example, molality is used when working with a range of temperatures. A one percent solution is defined as 1 gram of solute per 100 milliliters final volume.
For example, 1 gram of sodium chloride, brought to a final volume of 100 ml with distilled water, is a 1% NaCl solution. To help recall the definition of a 1% solution, remember that one gram is the mass of one milliliter of water. The mass of a solute that is needed in order to make a 1% solution is 1% of the mass of pure water of the desired final volume. Examples of 100% solutions are 1000 grams in 1000 milliliters or 1 gram in 1 milliliter. Perhaps the easiest way to describe a solution is in terms of weight-in-weight (w/w). The weight of the solute relative to the weight of the final solution is described as a percentage.
How To Find Moles From Volume Without Concentration For example, suppose you have a dye that is soluble in alcohol. Rather than write the instructions, "take 3 grams dye and mix with 97 grams absolute alcohol," you can describe the solutions simply as 3% dye in absolute alcohol. The formula applies to any volume of solution that might be required. Three grams dye plus 97 grams alcohol will have final weight of 100 grams, so the dye winds up being 3% of the final weight. Note that the final weight is not necessarily equal to the final volume.
Aqueous weight-in-weight solutions are the easiest to prepare. Since 1 milliliter of water weighs one gram, we can measure a volume instead of weighing the solvent. A very common use of w/w formulas is with media for the culture of bacteria. Such media come in granular or powdered form, often contain agar, and often require heat in order to dissolve the components. Microbiological media, especially when they contain agar, are difficult to transfer from one vessel to another without leaving material behind. They coat the surfaces of glassware, making quite a mess.
Using a w/w formula the media and water can be mixed, heated, then sterilized, all in a single container. Very little material is wasted and there is less of a mess. Molarity is moles of solute divided by liters of solution, not solvent. Here we've just calculated an approximate molarity, but the volume effect of adding a small amount of solute to water is usually small, so this calculation probably isn't too bad. The molarity is the number of moles of solute per liter of solution.
Molarity is defined as the number of moles of solute per unit volume. The molarity is reported as M , which is mol of solute/L of solution. Molarity is temperature dependent as the volume of the density of a solution typically changes with temperature. The definition of molarity means that you can find the molarity of a solution if you know the total number of moles of the solute and the total volume of the solution. So, in order to calculate the concentration of a solution , you need to divide moles of solute by total volume.
In an ionic solution, ionic strength is proportional to the sum of the molar concentration of salts. Molar concentration is a measure of the concentration of a chemical species, in particular of a solute in a solution, in terms of amount of substance per unit volume of solution. In chemistry, the most commonly used unit for molarity is the number of moles per liter, having the unit symbol mol/L or mol⋅dm−3 in SI unit. A solution with a concentration of 1 mol/L is said to be 1 molar, commonly designated as 1 M. To avoid confusion with SI prefix mega, which has the same abbreviation, small caps ᴍ or italicized M are also used in journals and textbooks.
The molarity calculator calculates the mass of compound required to achieve a specific molar concentration and volume. To dilute a solution of known molarity, please use the Solution Dilution Calculator. To dilute a solution of concentrated acid or base of known w/w% strength, please use the Acid & Base Molarity Calculator. We then convert the number of moles of solute to the corresponding mass of solute needed.
Both terms are used to express the concentration of a solution, but there is a significant difference between them. While molarity describes the amount of substance per unit volume of solution, molality defines the concentration as the amount of substance per unit mass of the solvent. In other words, molality is the number of moles of solute per kilogram of solvent . The units of molar concentration are moles per cubic decimeter. They are noted as mol/dm³ as well as M (pronounced "molar").
In many older books or articles, you can find different units of molar solutions – moles per liter (mol/l). Remember that one cubic decimeter equals to one liter, so these two notations express the same numeric values. When we describe a concentration as a percentage without specifying the type of formula, we imply that the solution is to be made using the weight-in-volume (w/v) method. As with w/w, weight-in-volume is a simple type of formula for describing the preparation of a solution of solid material in a liquid solvent.
A mole fraction, as the name implies, is a comparison of the number of moles in solution. It is found by taking the number of moles of solutes divided by the total number of moles (solutes + solvent). So you are not confused with similar chemical terms, keep in mind that molarity means exactly the same as molar concentration . It is defined as the number of moles of a substance or solute, dissolved per liter of solution (not per liter of solvent!).
This molarity calculator is a tool for converting the mass concentration of any solution to molar concentration . You can also calculate the mass of a substance needed to achieve a desired molarity. This article will provide you with the molarity definition and the molarity formula. This figure ( → ) shows how to make an X-molar solution, where X is the desired molar concentration.
The solute is dissolved in a smaller volume of solvent, then the total volume is adjusted to the final desired amount. The amount in moles of solute or the mass in grams of solute in a given volume of solution can be calculated from its concentration in mol/dm³. Molecules in a litre or even a cubic centimetre is enormous, it has become common practice to use what are called molar, rather than molecular, quantities.
A mole is the gram-molecular weight of a substance and, therefore, also Avogadro's number of molecules (6.02 × 1023). Thus, the number of moles in a sample is the weight of the sample divided by the molecular weight of the substance; it is also the number of molecules in the sample divided by Avogadro's number. Concentration in moles per litre (i.e., molarity) is usually designated by the letter M.
Molarity is a unit of concentration, measuring the number of moles of a solute per liter of solution. The strategy for solving molarity problems is fairly simple. This outlines a straightforward method to calculate the molarity of a solution. To find the concentration of this new solution you need to convert from grams to moles. This requires the use of the molar mass (given in grams/mole) of the NaCl. The molar mass of a substance is found by adding together the molar mass of the individual components.
Now you should have a good understanding of solutions and the solvation process for ions in aqueous solutions. You need to be comfortable with using molarity, molality and mole fractions. Also you should know the definitions pertaining to solutions. When discussing solutions, we typically talk about the solution's concentration.























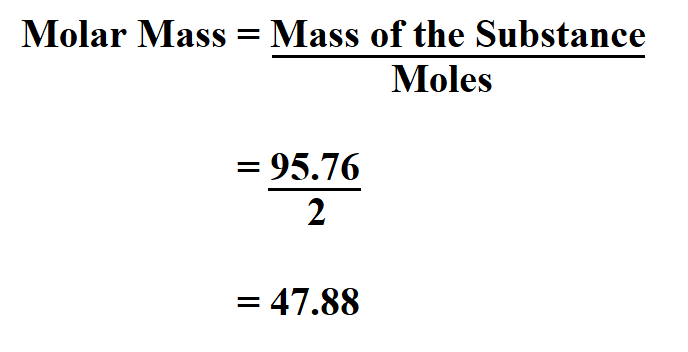


No comments:
Post a Comment
Note: Only a member of this blog may post a comment.